経済統計の使い方では、統計データの入手法から分析法まで解説しています。

不偏分散は母分散の推定値
分散はデータの散らばり具合を表すものです。母集団のデータがわかっている場合は、「偏差の二乗和をサンプル数で割る」ということで、計算できます。これが母分散です。
ここまでは理解できるのですが、標本から計算する母分散の推定値(不偏分散)は、「偏差の二乗和をサンプル数ー1で割る」ことで求められます。なぜ、1引くのでしょうか?今回は、それを説明します。
標本分散の計算法は母分散と同じ
標本から計算する分散なのになぜ不偏分散というのでしょうか?標本からとった分散なので、標本分散と言うのが自然だと思います。しかし、標本分散は違う意味で使われます。標本分散は、標本を使って母分散と同じ計算法をした場合の分散を言います。母分散と同じで、「偏差の二乗和をサンプル数で割る」ということです。ややこしいですね。
| 母分散 | 母集団の分散 |
|---|---|
| 不偏分散 | 標本を使った母分散の推定値 |
| 標本分散 | 標本を使って母分散と同じ計算方法をした分散 |
標本分散は母分散より小さい
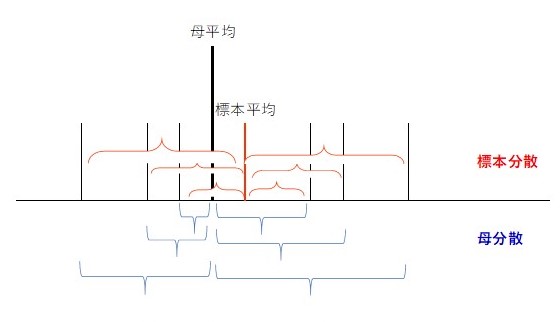
本当の平均(母平均)がわかっている場合、そこからの偏差を計算して分散が計算できます。しかし、母平均がわからない場合、標本平均を使うことになります。標本平均は、標本から計算した平均なので、標本平均の周りに均一に分布しています。一方、標本は母平均の周りに均一に分布しているわけではありません。そこのため、標本分散は、母分散より小さくなります。それを図示すると下記のようになります。
標本分散の期待値を計算
では、標本分散は、母分散よりどれくらい小さいのでしょうか。これは、標本分散の期待値を計算することでわかります。母分散を $σ^2$ とすると以下の式で表せます。この計算過程が非常に重要です。統計学の教科書などを参考にしてください。
$ \frac{n-1}{n} σ^2 $
ということは、小さくなった分を修正した分散、つまり、$\frac{n}{n-1}$をかけたものが適切な推定値となります。
$ 標本分散×\frac{n}{n-1}=\frac{偏差の二乗和}{n}×\frac{n}{n-1}=\frac{偏差の二乗和}{n-1} $
これが不偏分散で、偏差の二乗和をn-1で割ったものになります。