経済学Q&A　2024　その２

ミクロ５、６とマクロ１，２

ミクロ経済学

(長期平均費用）「様々な短期平均費用の最下点を結んだものになるはず」の最下点と、短期平均費用の最低点とは違うということですか？ならば最下点とは何でしょう？　

紛らわしい書き方でした。修正します。

「長期の平均費用」

様々な短期平均費用曲線の下側が形作る曲線（包絡線）。短期平均費用曲線の最低点を通るわけではない。

総費用について、教科書には以下のように書いてあります。

さまざまな短期総費用の下側が形づくる曲線となるわけである。このとき、長期総費用曲線は短期総費用曲線の包絡線であるという。

『ミクロ経済学の力』

短期と長期の費用曲線の関係（122枚目）について見ましたが、「平均費用が接する生産量で限界費用が交わる」ことが何を意味するのかよくわかりませんでした。単にそうなるというだけでしょうか。

長期の企業行動では生産量に応じた最適な生産設備があって、その中で最適な生産設備で生産します。その生産量では、

• 長期限界費用曲線は短期限界費用曲線と交わる
• 長期平均費用曲線は短期平均費用曲線に接する

ということですが、それ以上の意味はないと言えばないです。

次も参考にしてください。

【経済学】長期費用曲線と短期費用曲線の違いのまとめ－総費用、平均費用と限界費用 長期総費用曲線は、短期総費用曲線の包絡線 長期平均費用曲線は短期平均費用曲線の包絡線 長期限界費用曲線は、短期限界費用...

生産性と人件費の関係は式にするとどのような関係になっていますか。

生産性は、生産量／生産要素で表され、労働生産性は生産量／（就業者数×労働時間）です。ということで人件費とは直接の関係はないです。

ある財の限界費用と可変費用のグラフは同じになるということでよろしいでしょうか。

可変費用は総費用の一部です。総費用＝固定費用＋可変費用。限界費用は、生産追加1単位当たりの総費用の増加分です。

変動費用を労働力で考えた場合、限界費用は逓増しますが、材料費で考えた場合は大量仕入によるスケールメリットにより逓減するのでしょうか。

ここで考えているのは、生産要素の増減なので、短期では労働力の増減、長期では労働力と資本の増減を考えます。材料費は現実には費用として扱いますが、生産要素ではないので、考慮しません。

装置産業における入場者数とはどのようなものでしょうか。一般的に装置産業とは固定費用が大きい製造業、電気・ガス・水道業等を指すものと認識していましたが、間違いでしょうか。

テーマパークを装置産業として捉え、入場者数を生産量として捉えたためこのような問題になりました。わかりにくいたとえでした。

直感的に平均費用が低いほどよいというイメージがありましたが、そうではないということがわかりました。ただ、まったくもって平均費用は利益最大化と関係ないとは思えないのですが、利益最大化と平均費用には関係はないのでしょうか。

新規参入を考慮すると、価格が平均費用の最下点になったところで生産することになります。限界費用とも等しいですが。

平均費用と市場価格に関するグラフについて、新規参入（＝市場全体の生産量増大）によって市場価格が低下するとありましたが、1社の生産量を増加することによっても市場価格は低下、すなわち、市場価格の直線は右下がりとなるのではないでしょうか。

資本設備が一定の場合、1社の生産量を増やすと利益最大化が達成できないので、他社の参入が必要になります。

利潤がある限り新規参入企業があり、価格低下が均衡点まで進むとのことですが、均衡点に至ると旨味がない市場となるので、新規参入は止み価格変動も止まると考えるということでいいですか。

それで合っています。

新規参入のところが実際は利潤がなくなるまで企業が参入する場合はないと実際の社会では思いますがそれはなぜでしょうか？

たしかに完全に利潤がなくなれば参入しません。価格が平均費用の最低点に移動したとしても、最低限獲得したいと考えている利潤（正常利潤）は得られていると考えます。

以下を参考にしてください。

経済学では、参入という現象を考えるため、正常利潤という概念を用います。正常利潤とは、企業が最低限獲得したいと考えている利潤の水準で、これを超えた利潤を稼いでいる 企業があるような産業では参入が起こりますが、正常利潤以下の利潤しか稼げないような 産業には参入は起こらないであろうという限界的な利潤の水準のことです。

伊藤元重『ミクロ経済学　第２版 』

限界生産力逓減の法則が成り立つのはあくまで１つの生産要素だけを増やした時だけで、全部の生産要素を増やせばその法則は成り立たないという理解でよろしいでしょうか。（DVDの内容でいうところの若衆だけでなく臼や杵も増やした場合は倍の生産数になったというところ）

そうですね。両方増やせば生産は増えます。逓減はしません。コブダグラス型の生産関数では、若衆を２倍にし臼や杵を２倍にすれば、生産も２倍になります。

たとえばディズニーランドのようなテーマパークの場合、キャストの数は有限で無限には増やせないので費用はある値で有限になるように思いますが、限界費用や平均費用は収束するように思いますが、平均費用はかならずU字で、限界費用は必ず右上がりになるのでしょうか。

その場合は、供給量の制約（有限のキャストの数）があるまで限界費用が増え続けるということになります。

平均費用の場合はU字型なので、供給制約がどこにあるかによって結果が違っていて、最低点よりも生産量が少ないところに供給制約がある場合は、平均費用は下がり続けることになります。

電力業や鉄道など、固定費が非常に大きい産業は、生産量を増やしてもなかなか平均費用の最低点まで到達しません。そのような産業を費用逓減産業と呼びます。

コブダグラス型の生産関数において、資本と労働力の労働分配率を資本0.3と仮定していますが、もし、この分配で計算を行うこととなった根拠や裏話をご存じでしたら教えていただきたいです。

SNAベースでの労働分配率はだいたい70％なので、この数字を仮定しています。以下のディスカッションペーパーなどを参考にしてください。

田中・菊池・上野「近年の労働分配率低下の要因分析」経済財政分析ディスカッション・ペーパー

操業停止点まで価格が下がった場合、操業停止・撤退などが起こることで、そのうちに市場価格は損益分岐点に戻るということですか。

企業は赤字になるので、撤退する企業が増え、供給量が減って、価格が上昇すると思います。

今回でミクロ経済学が終わりかと思いますが、小テストでもしばしば誤答してしまっているのでもう少し練習問題に触れたいと考えております。なにか参考書等ございますでしょうか。

練習問題という意味では、公務員試験　新スーパー過去問ゼミが良いと思います。

読み物として面白いという意味ではクルーグマンの「ミクロ経済学」などをお勧めします。

マクロ経済学

農家の自家消費はどのように算出されているのでしょうか

農林水産省「農業・食料関連産業の経済計算」などを使うようです。ただ、以前の資料には数値がありますが、最近の資料では明示的には示されていません。

コメについては、生産者の米穀在庫等調査結果に自家消費額が載っています。

（参考）農業所得の捕捉率について

農林水産省『農業・食料関連産業の経済計算』では、農産物等の自家消費が「農業中間投入」と「農家の家計消費」に区別して掲載されている。

「農業所得の捕捉率について」

帰属計算は欠測値を補完するために行うと思いますが、帰属計算の例外として挙げられた各項目は、欠測値とはみなされず、他のなにかしらの分類でGDPにカウントされているのでしょうか。

そうです。以下のようになります。

• 公務員の業務→政府最終消費支出
• 農家の自家消費分、医療費の社会保険分、持ち家のサービス→家計最終消費支出
• 企業の現物支給→雇用者報酬

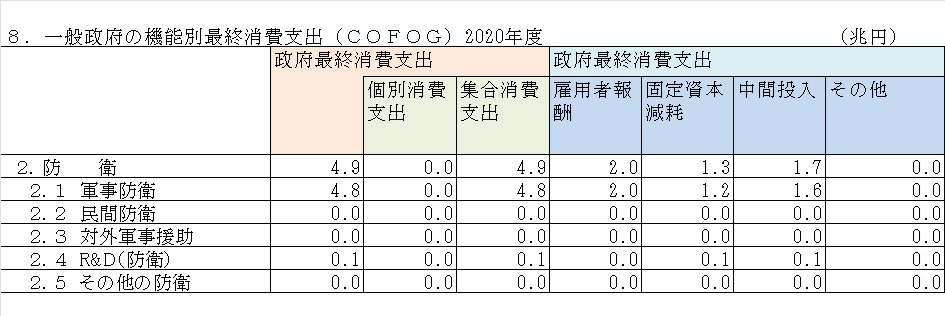
帰属計算について、防衛関係費は支出金額をもとにGDPに含まれるとのことであったため、昨今の防衛費増額によってGDPがどの程度変化するのか調べてみたいと思った。

政府最終消費支出の内訳はGDPの内訳として載っています。機能別最終消費支出

公務員の業務は、支出額で計算するので、

公務員の給与→雇用者報酬

政府の支出（事務用品など）→中間投入

となります。通常は中間投入は差し引きますが、政府サービスの生産の一部と考えます。戦車などは、公的固定資本形成になります。

株価や土地の価格上昇について、GDPとどのように影響あるか話したほうがいいかと思います。

GDPは新たに生み出した価値（付加価値）を計上します。株価や土地の値上がりは、資産価格の上昇であって、新たな価値を生み出していないので、GDPには影響しません。

帰属計算をする財・サービスについて、明確な基準があればご教示いただきたいです。

帰属計算した方が理論的にあっていて、影響が大きい（額の大きい）ものだと思います。

ビデオの最後のお客さんは先生ですか。

違います。ディレクターの方です。

サービス業の付加価値は、生産額となるでしょうか

生産額になります。

産業別の国内総生産などを参考にしてください。

三面等価の原則について、生産と消費の時点が異なっていても成り立つのでしょうか。例えば、2000年に生産したものを2001年に消費した場合、2000年と2001年のGDPは消費の面からみると異なるのではないでしょうか。

ぴったりは合わないですね。統計上の不突合という項目があります。

数量も金額も比較年の数値を使用する場合はあるのでしょうか。

分子を比較年の数量×価格、分母を基準年の数量×価格とすると、

比較年の名目消費額／基準年の名目消費額

となって、名目消費額の指数となり、価格指数にはなりません。

理想的な価格指数は、フィッシャー式と呼ばれ、ラスパイレス式とパーシェ式を使って作ります。

$ フィッシャー指数＝ \sqrt{ラスパイレス式　×　パーシェ式} $

問題と正解

生産関数は以下の通りです。

$𝑌=𝐴𝐾^{0.3} 𝐿^{0.7}$

これの対数をとります。

$log(𝑌)=log(𝐴)+0.3log(𝐾)+0.7log(𝐿) $

それを時間に関して微分します。

$　\dfrac{\Delta Y}{Y}=\dfrac{\Delta A}{A}+0.3 \dfrac{\Delta K }{K}𝐾+0.7 \dfrac{\Delta L}{L}$

これを言葉で表すと、

$経済成長率＝全要素生産性成長率＋0.3×資本ストック成長率＋0.7×労働投入量成長率$

となります。

全要素生産性を$ｘ$とすると、

$ 1=x+0.3×２＋0.7×（-2) $

$ X= 2.5 $

となります。

名目値は、通常の金額ベース、実質値は基準年の価格を基準として、価格の影響を除いたものです。基準年の価格指数は常に100です。

	名目値	実質値	価格指数
基準年	3000	3000	100
比較年	6000	3000	200

上の例では、基準年は、3000/100×100＝3000、比較年は、6000/200×100＝3000となります。

基準年の価格指数は常に100なので、実質値＝名目値／100×100＝名目値となり、基準年の名目値と実質値は等しくなる。